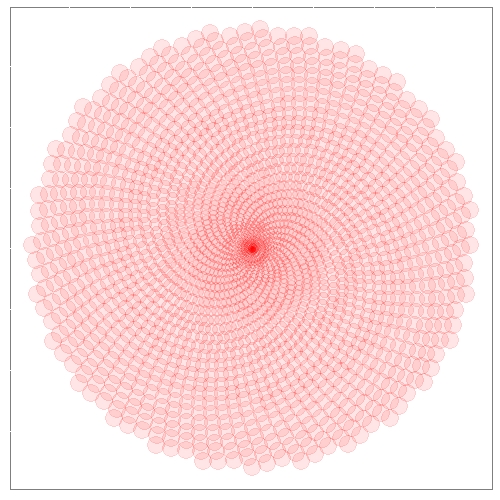
Patterns in nature

“A scientist does not study nature because it is useful; he studies it because he delights in it, and he delights in it because it is beautiful” - Henri Poincaré

There are many examples of natural facts that can be described in mathematical terms. Nice examples are the shape of snowflakes, the fractal geometry of romanesco broccoli or how self-similarity rules the growth of plants.

R is a tool for doing serious analysis, but not everything in life is serious. Life is also funny, and R can be used to have fun and to do beautiful things. Its graphical power can be used to produce artistic images like the one that illustrates this section, which is inspired by how plants arrange their leaves. This fact is called phyllotaxis and will serve as the basis of this project.

# This sets plot images to a nice size.
options(repr.plot.width = 4, repr.plot.height = 4)

# Loading in the ggplot2 package
library(ggplot2)

Drawing points on a circle

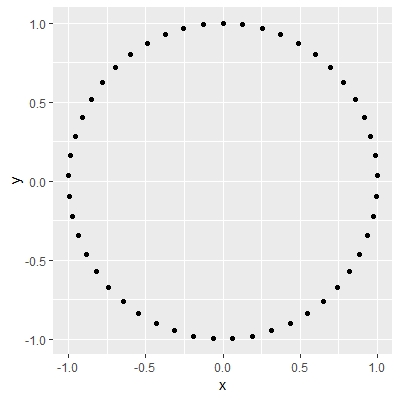
There are many ways to represent data with ggplot2: from simple scatter plots to more complex ones, such as violin plots. The functions that start with geom_ define how the plot is shown. We will only work with geom_point which plots points in two dimensions. We just need a dataset with two variables, let’s call them x and y.

Let’s start by drawing 50 points on a circle of radius 1. As every (x, y) point should be in the unit circle, it follows that x² + y² = 1. We can get this using the superfamous Pythagorean trigonometric identity which states that sin²(θ) + cos²(θ) = 1 for any real number θ.

# A sequence starting with 0 and ending with 2 times pi
t <- seq(0, 2*pi, length.out = 50)
x <- sin(t)
y <- cos(t)
df <- data.frame(t, x, y)

# Scatter plot of points in a circle
p <- ggplot(df, aes(x, y))
p + geom_point()

Making it harmonious with golden angle

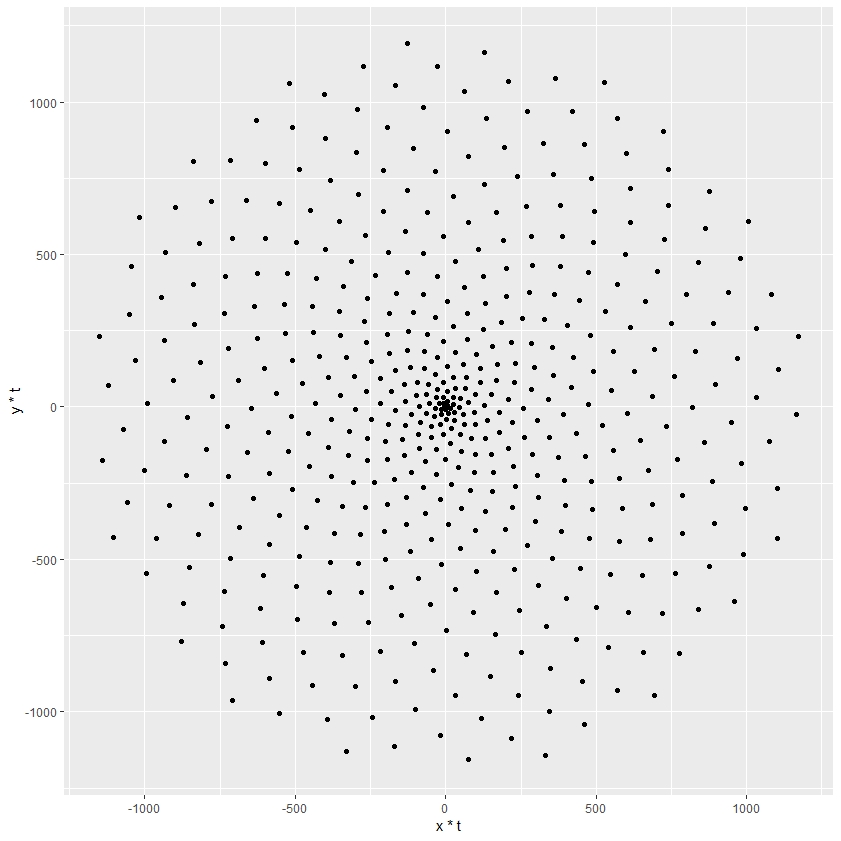
Plants arrange their leaves in spirals. A spiral is a curve which starts from the origin and moves away from this point as it revolves around it. In the plot above all our points are at the same distance from the origin. A simple way to arrange them in a spiral is to multiply x and y by a factor which increases for each point. We could use t as that factor, as it meets these conditions, but we will do something more harmonious. We will use the Golden Angle:

Golden Angle = π(3 − √5)

This number is inspired by the Golden Ratio, one of the most famous numbers in the history of mathematics. Both the Golden Ratio and the Golden Angle appear in unexpected places in nature. Apart of flower petals and plant leaves, you’ll find them in seed heads, pine cones, sunflower seeds, shells, spiral galaxies, hurricanes, etc.

It’s time to spiralize!

# Defining the number of points
points <- 500

# Defining the Golden Angle
angle <- pi*(3 - sqrt(5))

t <- (1:points) * angle
x <- sin(t)
y <-cos(t)
df <- data.frame(t, x, y)

# Scatter plot of points in a spiral
p <- ggplot(df, aes(x*t, y*t))
p + geom_point()

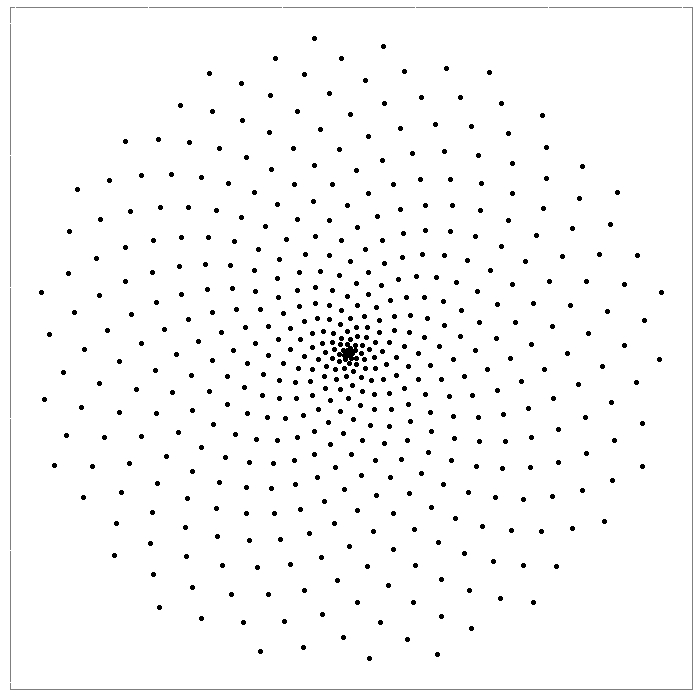
Apart from data, a plot includes many other components that define its final appearance. Our previous plot contains:

• a background filled with grey color.
• a grid of horizontal and vertical white lines in the background.
• ticks along the axis.
• a title on each axis.
• text along axes to label marks.

Art does not get along with most of these elements, so it’s time to move to action.

df <- data.frame(t, x, y)

# Scatter plot of points in a spiral with everything removed

p <- ggplot(df, aes(x*t, y*t))
p + geom_point() + theme(panel.background = element_rect(fill = "white", colour = "grey50"), 
                         panel.grid.major = element_blank(), axis.ticks = element_blank(), axis.title = element_blank(), 
                         axis.text = element_blank())

Adding size, color and transparency

Our drawing starts to look like a plant, but we can do it much better. By changing color, transparency (also called alpha), and size of the points, the image will become more appealing.

The Dandelion

Until now, all points have the same appearance (size, color, shape, and alpha). We mightl want to make the appearance of the points dependent on a variable in our dataset. Now we will make size variable. We will also change the shape of points. Although we won’t be able to blow on it, the resulting image should resemble a dandelion.

p <- ggplot(df, aes(x*t, y*t))
p + geom_point(aes(size = t), shape = 8, alpha = 0.5, colour = 'black') + theme(panel.background = element_rect(fill = "white", colour = "grey50"), 
                                                                                axis.ticks = element_blank(), axis.title = element_blank(), 
                                                                                axis.text = element_blank(), legend.position = 'none')

The Sunflower

Plants not only use the Golden Angle to arrange leaves. It is also found in the arrangement of sunflower seeds. We don’t need anything new to draw a sunflower.

p <- ggplot(df, aes(x*t, y*t))
p + geom_point(aes(size = t), shape = 17, alpha = 0.5, colour = 'yellow') + theme(panel.background = element_rect(fill = "darkmagenta", colour = "grey50"), 
                                                                                  axis.ticks = element_blank(), axis.title = element_blank(), 
                                                                                  axis.text = element_blank(), legend.position = 'none')

These patterns are very sensitive to the angle between the points that form the spiral; small changes to the angle can generate very different images. Let’s look at an example of that.

angle <- 2.0
points <- 1000

t <- (1:points)*angle
x <- sin(t)
y <- cos(t)

df <- data.frame(t, x, y)

p <- ggplot(df, aes(x*t, y*t))
p + geom_point(aes(size = t), shape = 17, alpha = 0.5, colour = 'yellow') + theme(panel.background = element_rect(fill = "darkmagenta", colour = "grey50"), 
                         axis.ticks = element_blank(), axis.title = element_blank(), 
                         axis.text = element_blank(), legend.position = 'none')

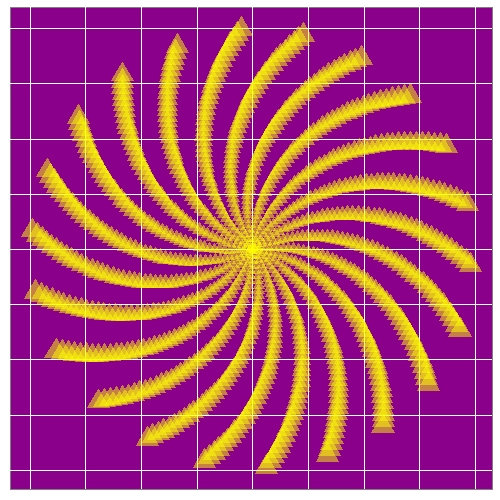
We can create an infinite number of patterns inspired by nature: the only limit is our imagination.